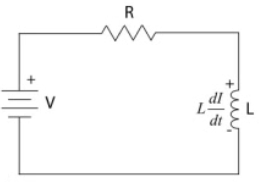
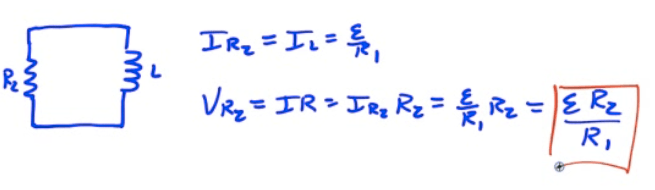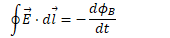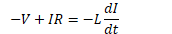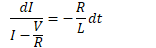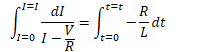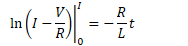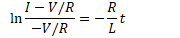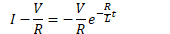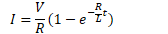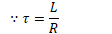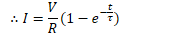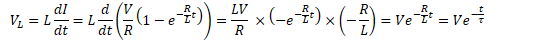Inductors in Circuits
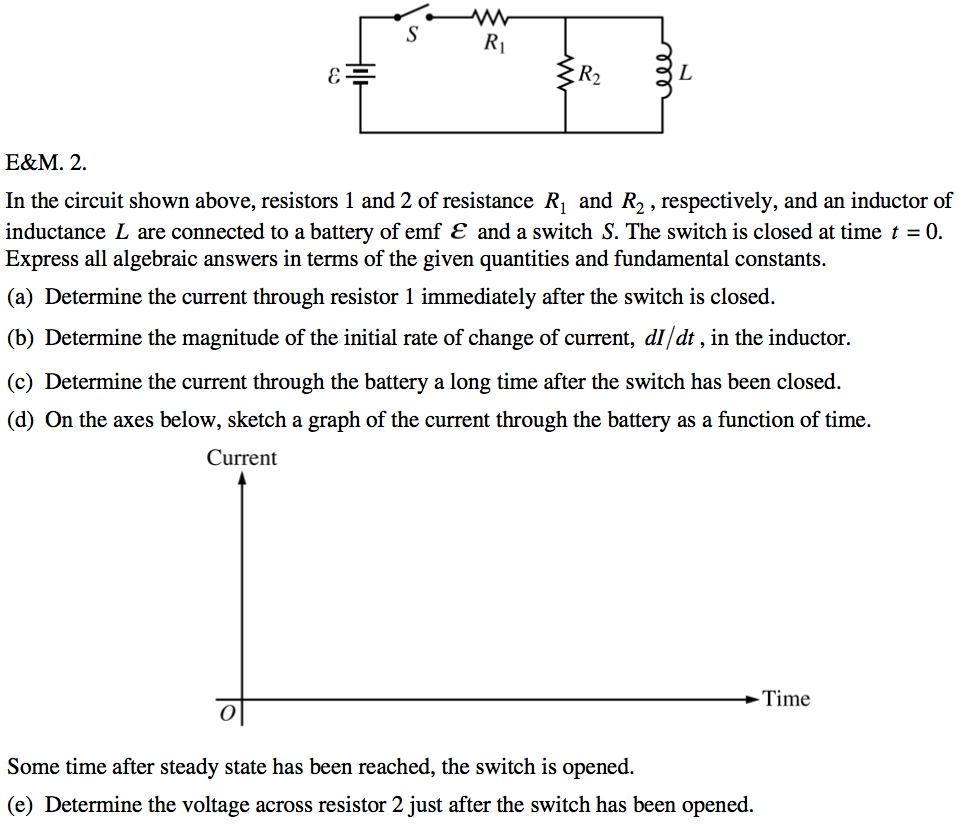
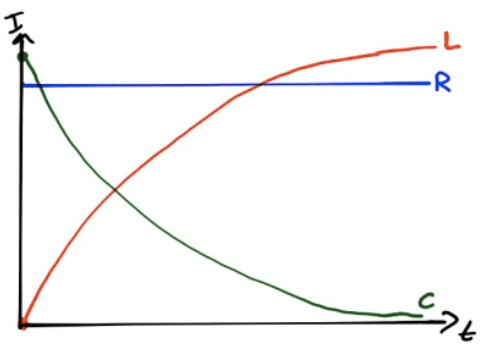
When circuit is first turned on, inductor opposes current flow and act like an open circuit
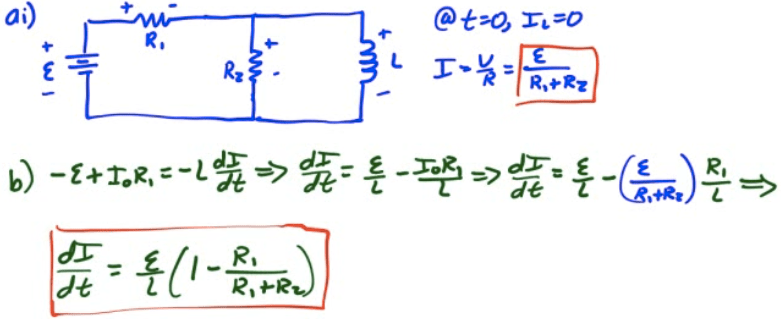
After a time, inductor keeps current going and acts as a short
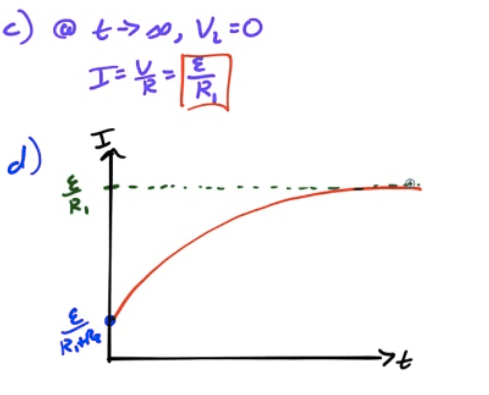
After a long time, if the battery is removed, the inductor acts as an emf source to keep the current going
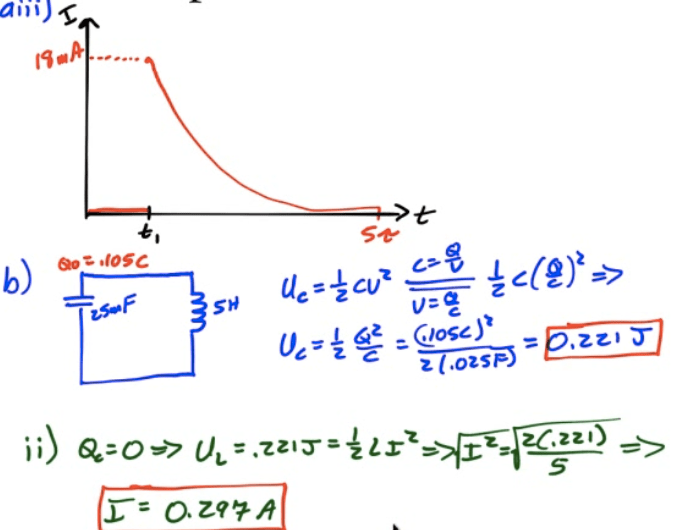
As the resistor dissipates power, the current will decay exponentially to zero.
Current in RL Circuits
Voltage in RL Circuits
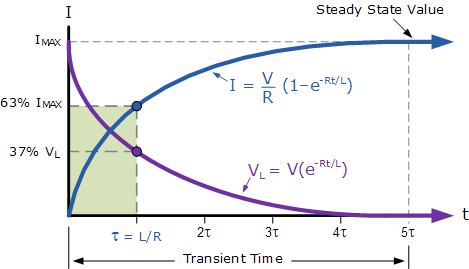
Current and Voltage Graphs
2011 Free Response Question 2
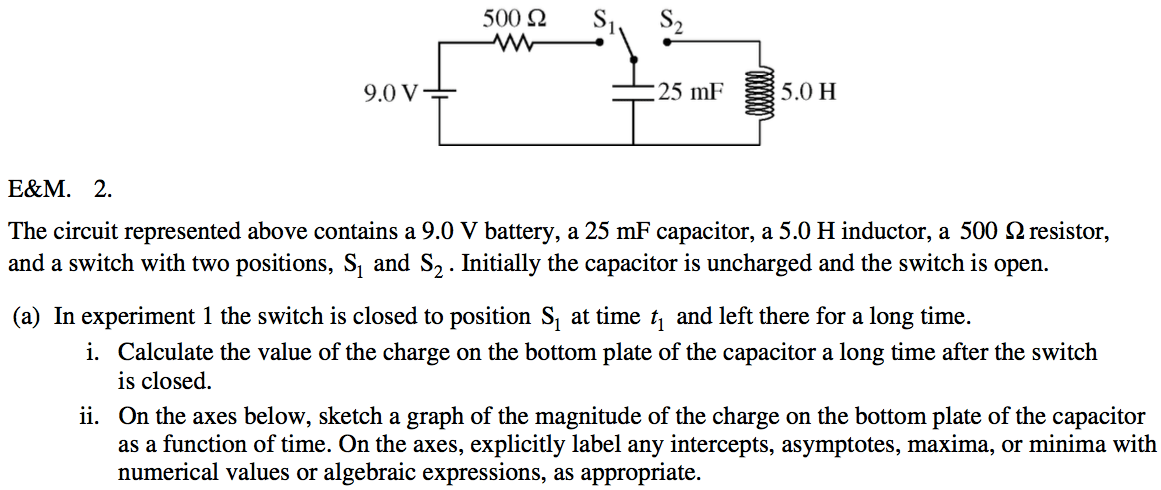
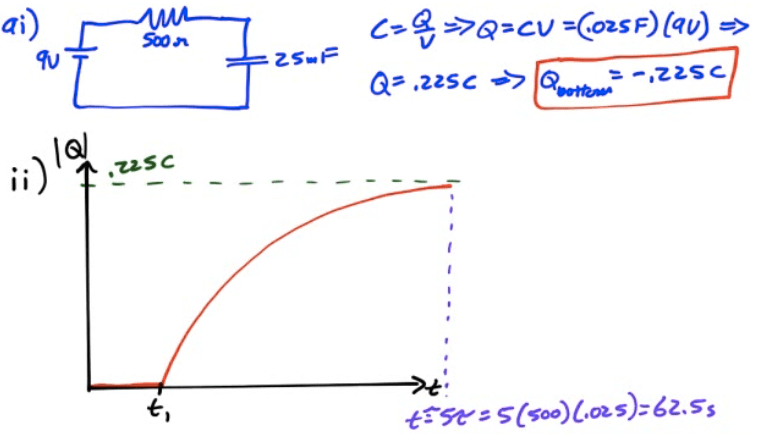


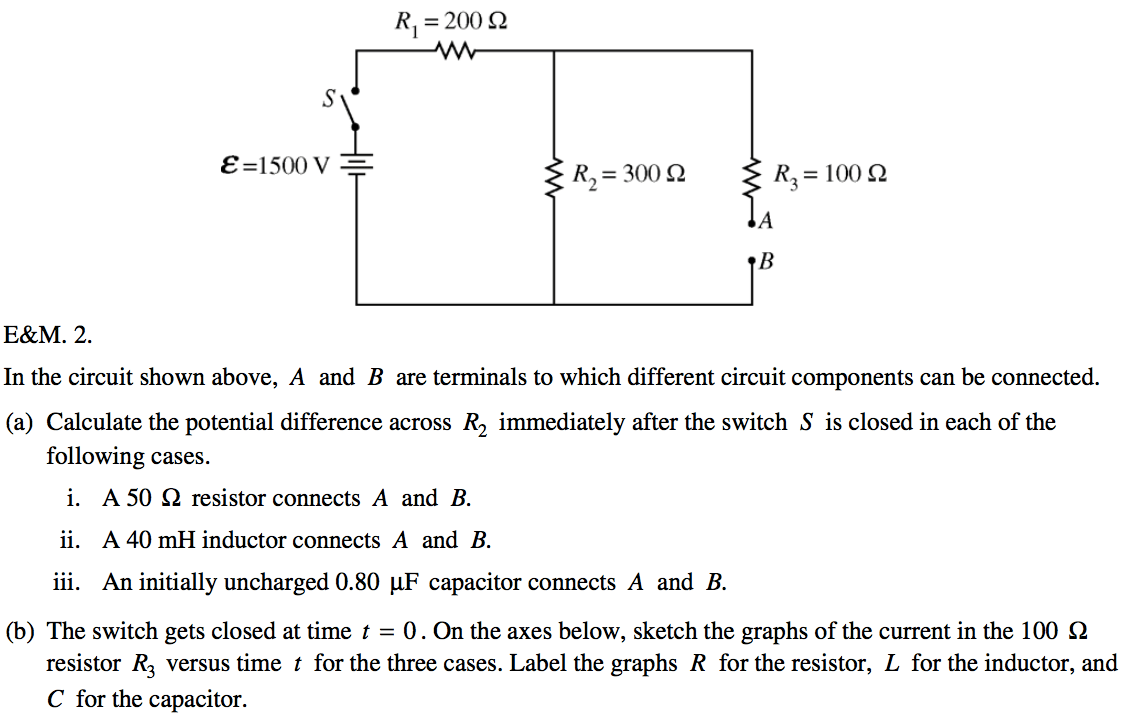
2008 Free Response Question 2
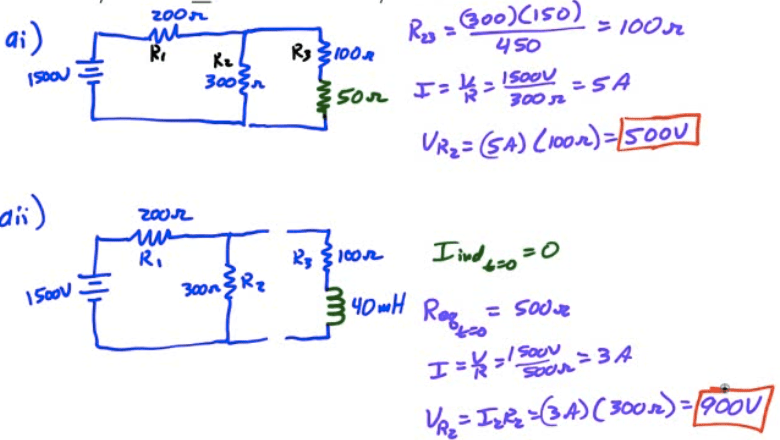
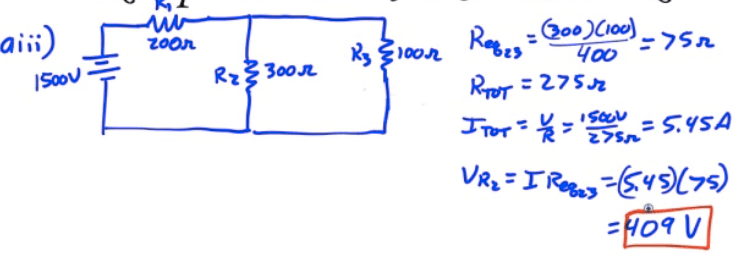
2005 Free Response Question 2